Skip to main content

Evo-BWB: Evolutionary Optimized Broken Wing Butterfly

· 8 min read

There aren’t many scientific publications on practical options trading. In this article, we will recreate the results of one of the few, titled: Differential Evolution Optimization of the Broken Wing Butterfly Option Strategy by David Munoz Constantine, Richard Tymerski, and Garrison Greenwood.

Note on naming

The authors did not provide a succinct name for the trade; We have named it Evo-BWB for easier reference.

Strategy overview​

The publication explores optimizing a Broken Wing Butterfly (BWB) options strategy using a Differential Evolution (DE) algorithm. This optimization is performed using over a decade of historical option data for the S&P 500 ETF (SPY), focusing on maximizing profitability while managing risk and volatility. After an initial optimization process, the authors execute a second round of (re-)optimization to reduce volatility. We will recreate their re-optimized results in this post.

Our opinion is that the publication is well-written and provides a good overview of both option trading and genetic optimization algorithms. We really appreciate that it offers a meaningful analysis of the results and includes a trade example. Unfortunately, the complete trade list (blotter) is not provided in the paper; therefore, we cannot cross-check our entries and exits with theirs.

As the article was published in 2020, there are four years of truly out-of-sample data available at the time of this writing. In our study, we will slightly differ in our simulation methodology from the original paper:

  • Instrument: SPX options instead of SPY options in the article.
    This change is due to data availability in MesoSim.

  • Timeframe and resolution: The authors used daily (EOD) data from between 2005 and 2016, obtained from IVolatility.
    We will be using intraday data from the CBOE between 2012 and 2024.
    To provide similar timing, we will schedule our entries and exits five minutes prior to the close.

  • Positions in flight: We will use four positions in flight, as opposed to one in the article.
    We believe having multiple positions in flight provides more stable results and reduces the chances of the strategy being either lucky or unlucky.

We believe that the differences listed above should not cause major deviations from the original in terms of strategy performance.

Strategy definitions​

Contract Selection ​

The expirations are always selected (optimized) using a fixed Days Till Expiration (DTE) approach. Strike selection, however, studies three distinct methods:

  • Points Map: Relative to underlying based on point (dollar) values.
  • Delta Map: Strikes selected based on Delta (greeks).
  • Normalized Map: Relative to underlying based on strike / underlying ratio.

Entry and exit​

In the publication, the authors not only optimize the contract selection process but also select the best entry and exit combinations using an evolutionary algorithm. Entries are also gated by specifying a 'Maximum Cost,' which can be calculated using the Credit Received / RegT Margin formula.

Exits are optimized such that the Profit Target (Min Profit %) and Stop Loss (Max Loss %) are specified as functions of PnL / Reg T Margin. Additionally, the maximum days in trade are also optimized, with an 'override':

If the underlying reaches a certain price level, then the position is taken to expiration.

Adjustments​

The strategy doesn’t have any adjustments.

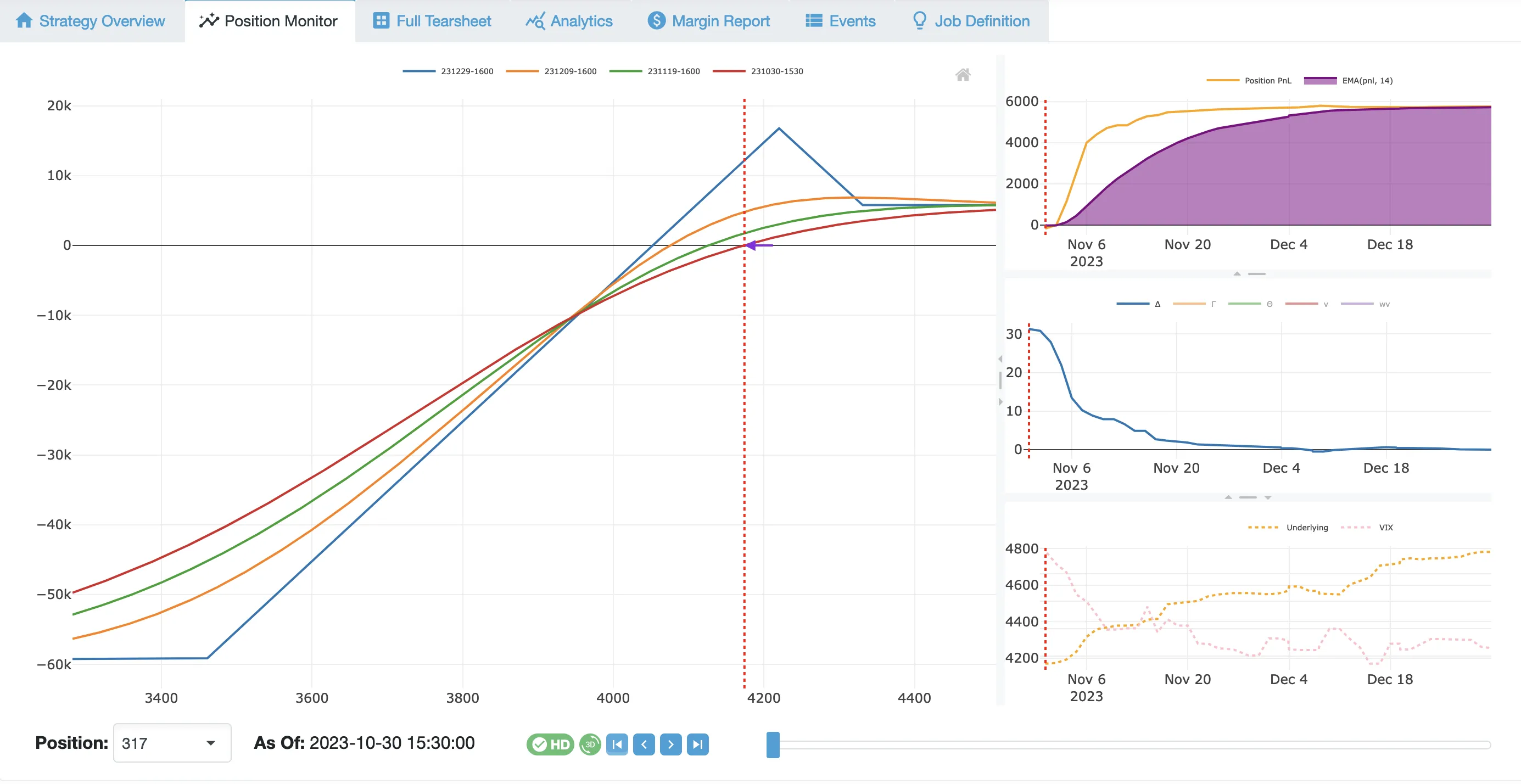
MesoSim results​

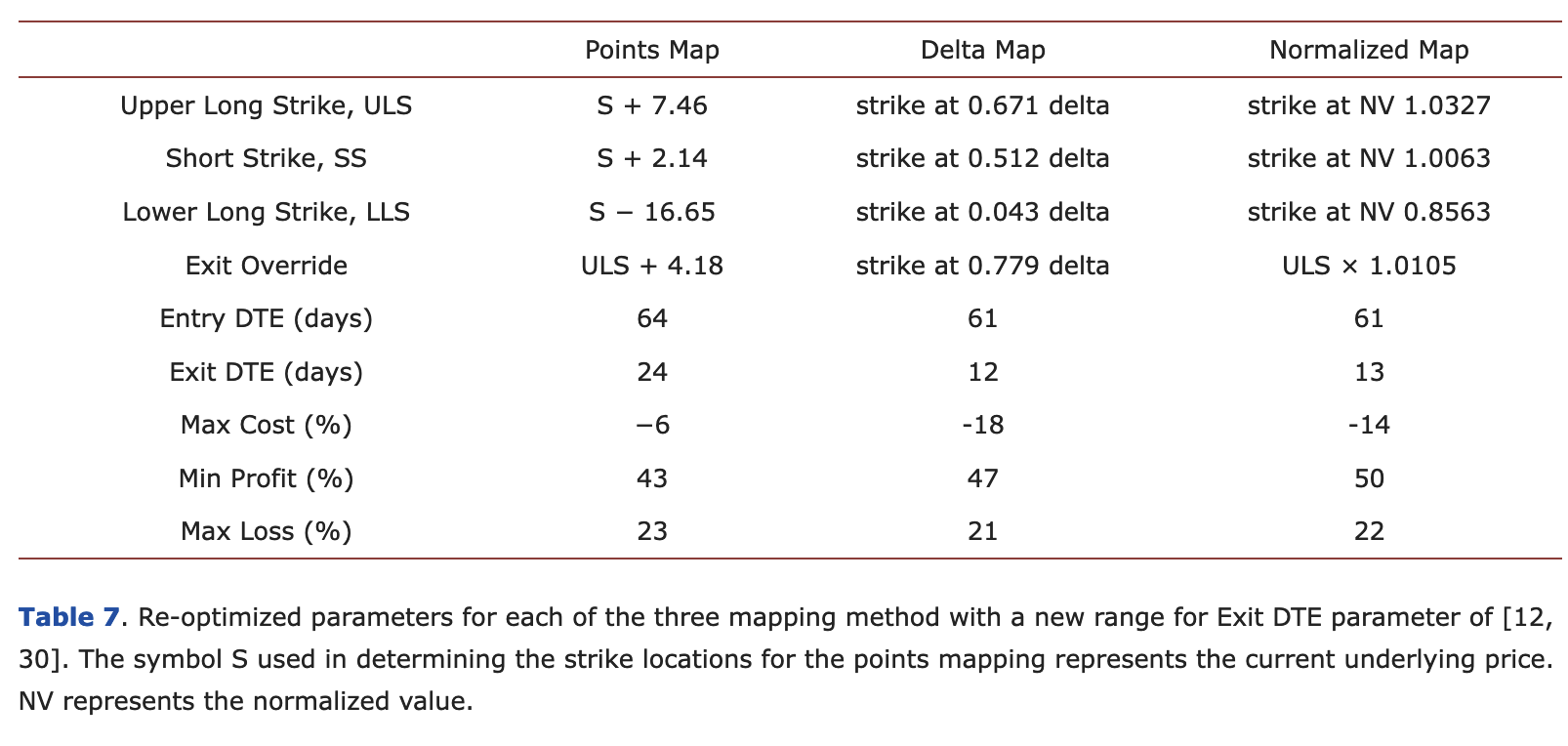
The following table (Table 7 in the original publication) summarizes the thresholds re-optimized to reduce volatility.

EvoBWB Strategy Definition Table

Points Map​

With the Points Map approach, the authors define the strikes based on point distance from the underlying. Two things to note here:

  • We need to account for the fact that we are working with SPX data which is 10 times the size of SPY.
  • In our opinion, this approach might not hold up too well over time as the underlying price increases.

The strikes can be defined using the Statement Selector:

"StrikeSelector": {
  "Statement": "underlying_price + (7.46 * 10)"
}

The entry gating mechanism is described using Entry.AbortConditions, while the exit criteria for the trade plan are expressed using Exit.ProfitTarget, Exit.StopLoss, and Exit.Conditions (for the MaxDIT).

The resulting run is here: https://mesosim.deltaray.io/backtests/e25deb5a-352f-4ff9-a79e-ab89a856c3cb

Please note that the backtest has an extended period during which the strategy is unable to enter any positions. This is due to the entry gating (implemented via Entry.AbortCondition in MesoSim), which uses the credit/margin relationship. We attribute this behavior to the difference between the SPY and SPX underlyings. Most importantly, in the recent period, the AbortCondition has consistently been true, prohibiting entries from October 2018 onwards.

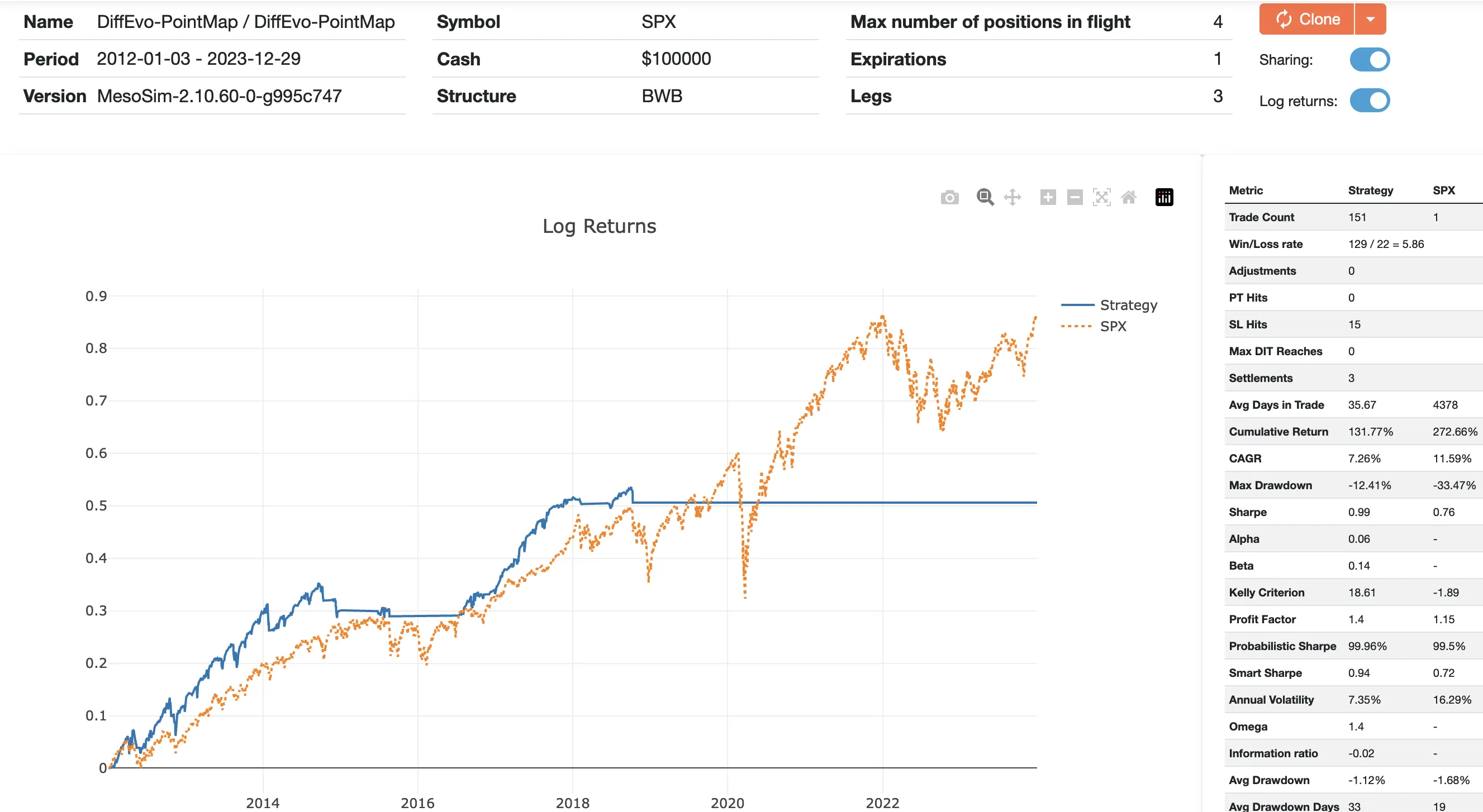
EvoBWB Points Map Overview

Given the extended period of non-trading times, it’s not worthwhile to analyze the strategy performance in detail.

Delta Map​

The delta-based strike selection is fairly standard in options trading strategies. Unlike the Points Map method, this selection doesn't require readjustments as the underlying grows in size.

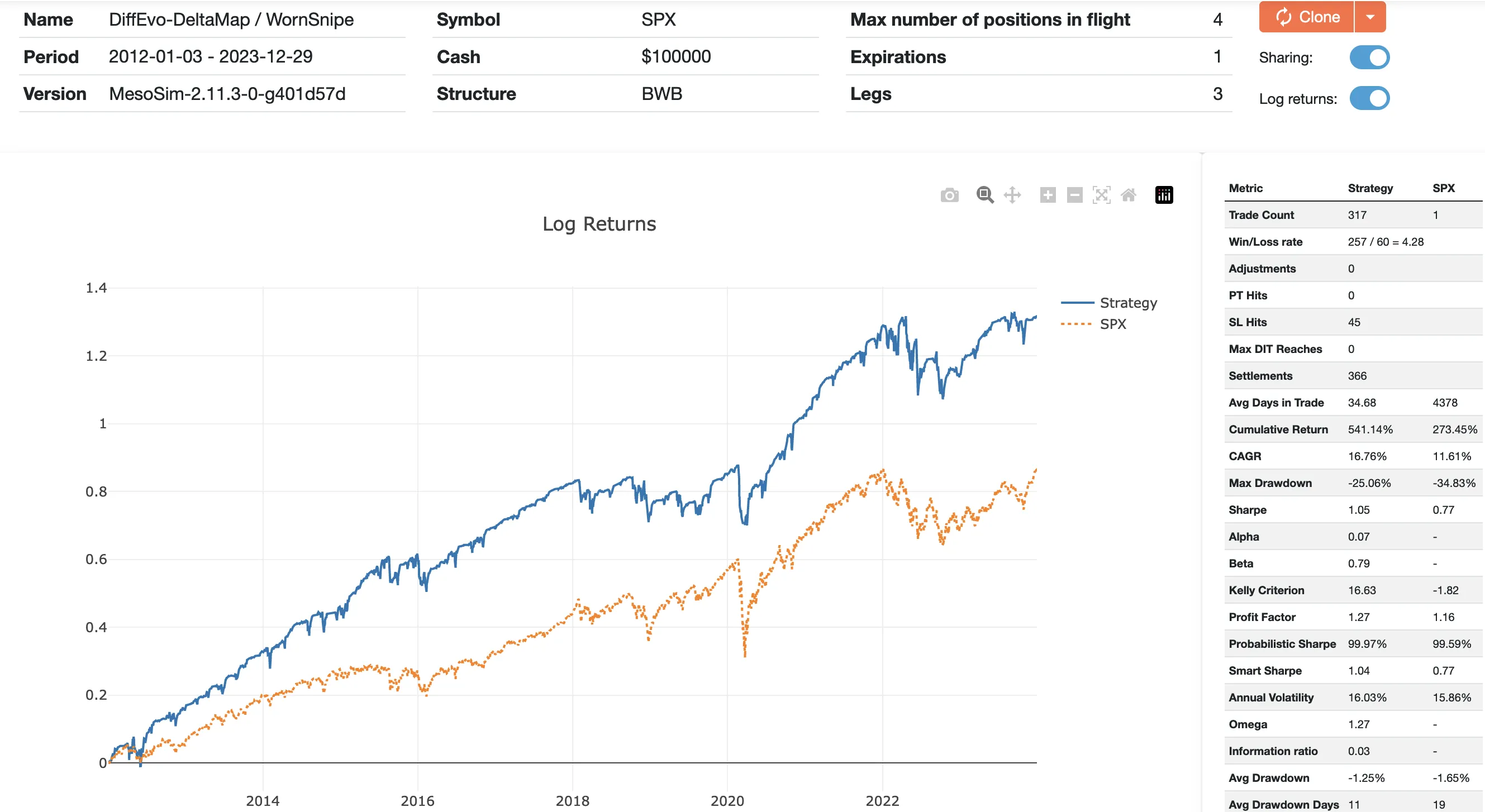
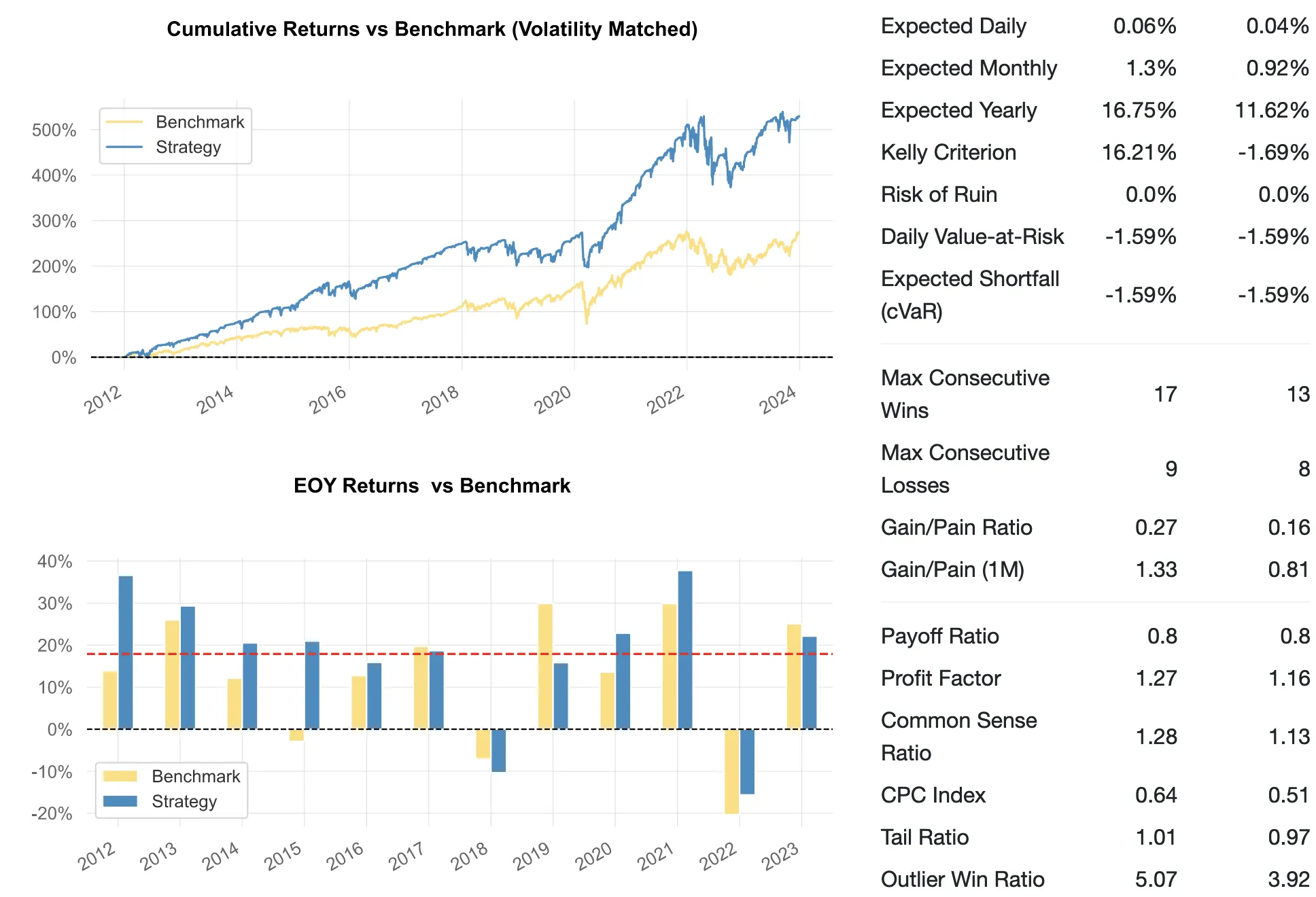
The resulting run is here: https://mesosim.deltaray.io/backtests/2468026e-ab56-4d4e-a975-3d217d57b3f4

EvoBWB Delta Map Overview
EvoBWB Delta Map Risk Graph
EvoBWB Delta Map Result Breakdown 1
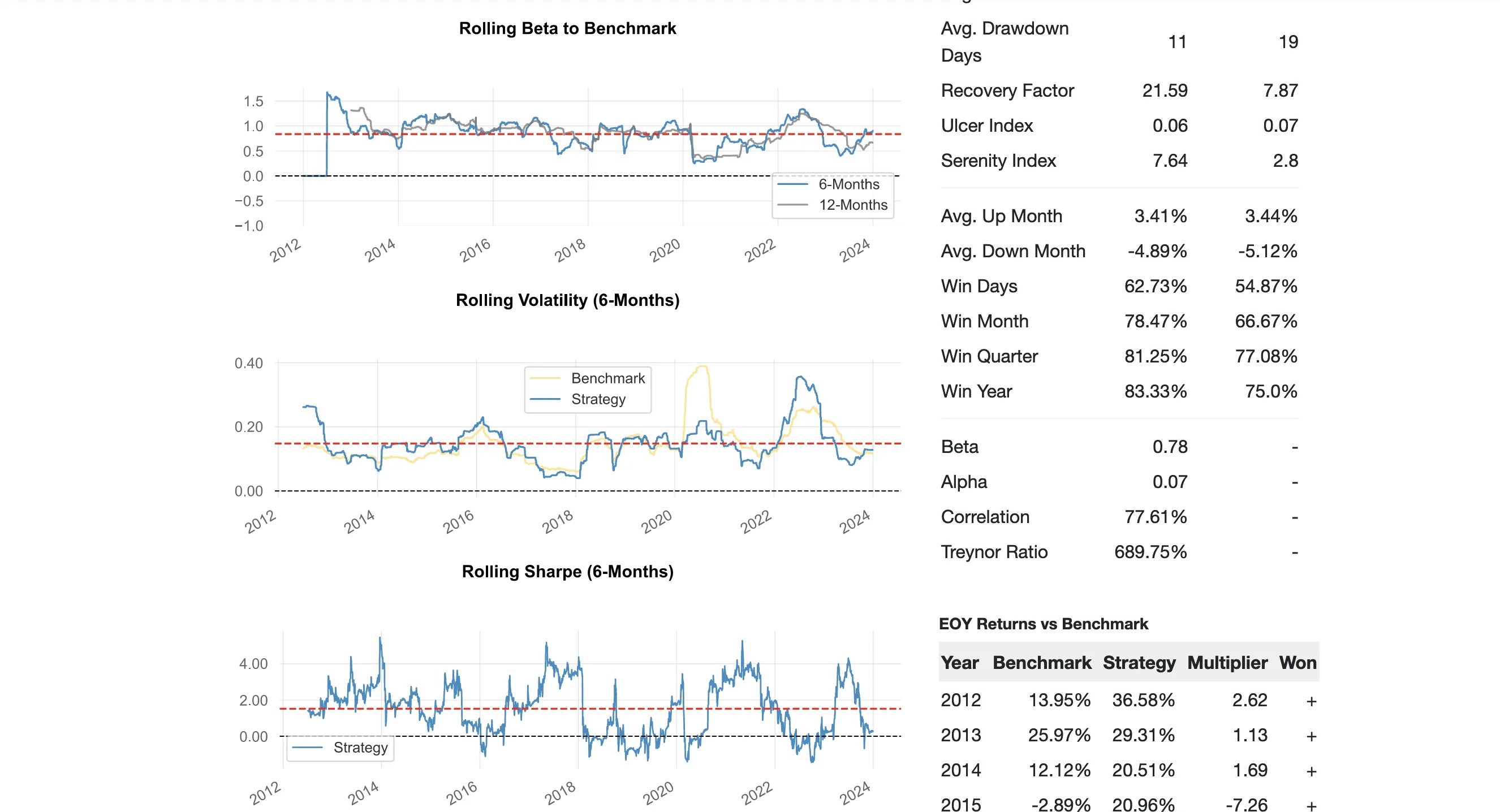
EvoBWB Delta Map Result Breakdown 2

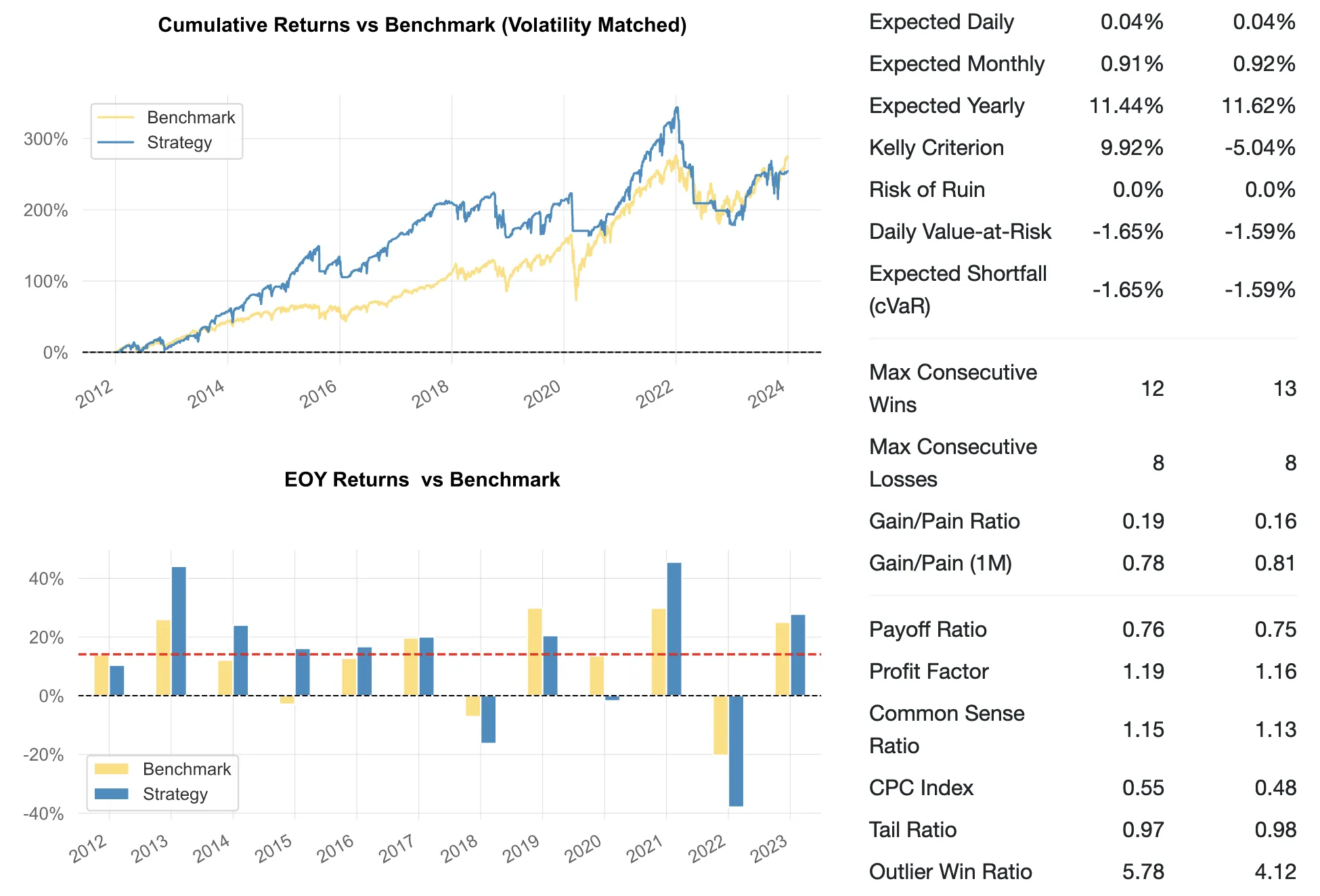
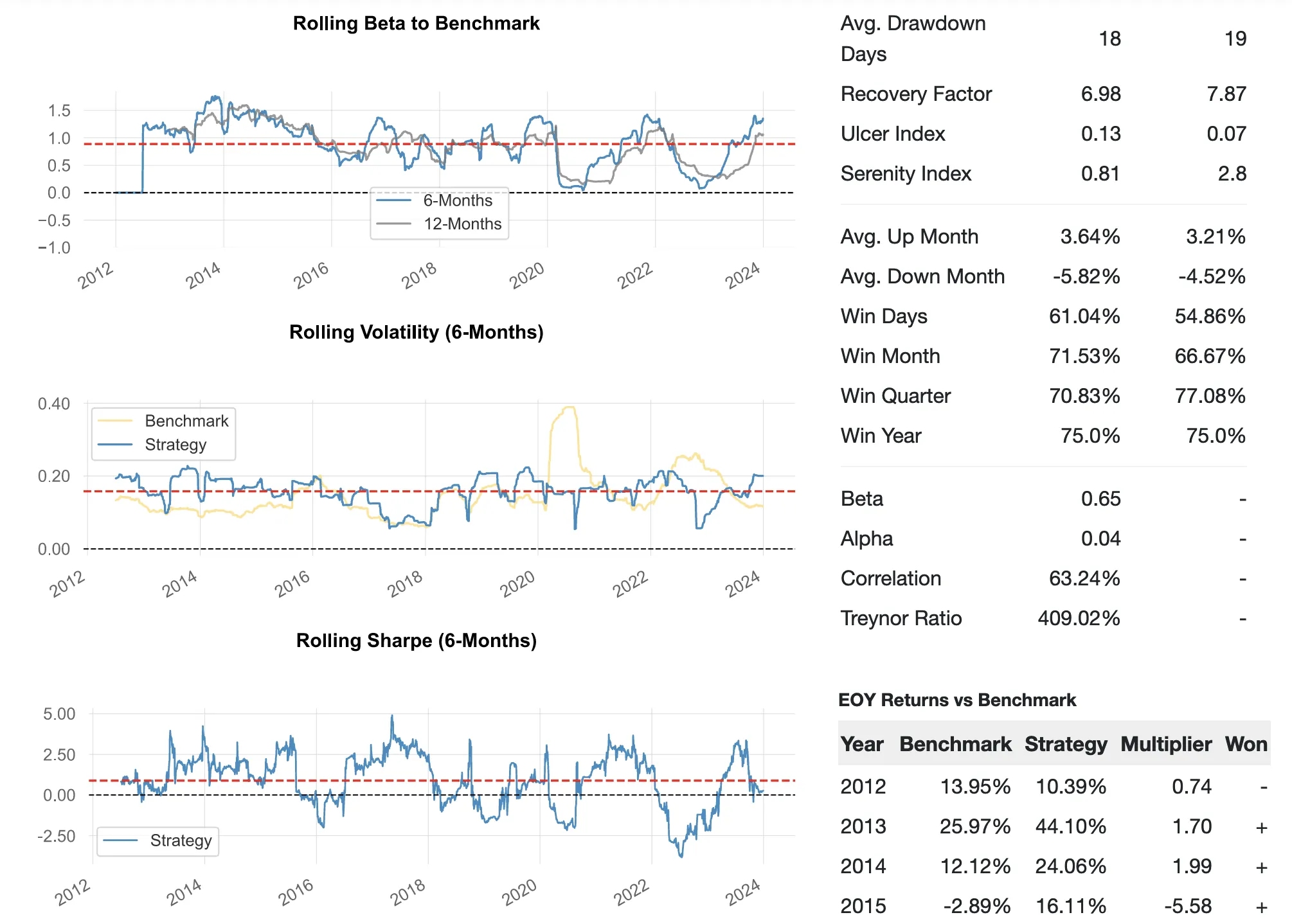
Based on quantitative metrics (Sharpe, Sortino Ratio, Alpha), the strategy slightly outperforms the buy-and-hold approach. Looking at Beta (and the PnL chart itself), it's apparent that the strategy has a substantial correlation with the buy-and-hold approach. 

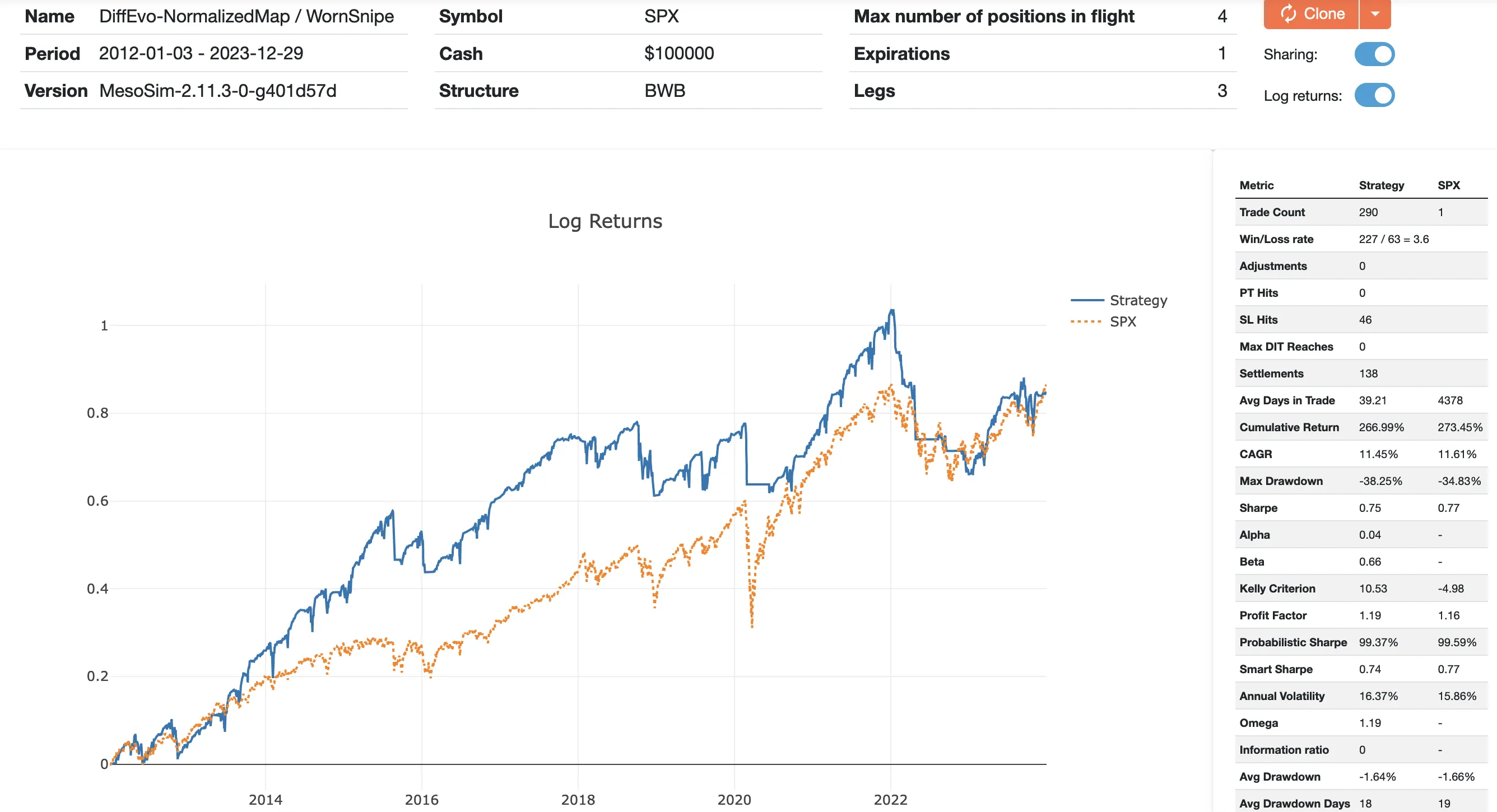
Normalized Map​

The same authors propose a novel method of strike selection based on the strike-to-underlying_price ratio. Their other publication shows that the normalized map approach provides superior performance compared to point- or delta-based strike selection. The normalized map-based strike selection can be implemented in MesoSim using the Complex Strike Selector. The Complex Strike Selector is capable of iterating through all contracts in the given expiration, computing a custom metric (such as strike to price ratio, covering the normalized approach here), and selecting the one closest to the target. Additionally, constraints (filters) can be used to exclude unwanted contracts using Lua statements.

Resulting run: https://mesosim.deltaray.io/backtests/13abc0ba-9fc7-4dc5-95d4-f1136af16b1b

EvoBWB Normalized Map Overview
EvoBWB Normalized Map Risk Graph
EvoBWB Normalized Map Result Breakdown 1
EvoBWB Normalized Map Result Breakdown 2

The run shows that the strategy's performance (in terms of Sharpe) is slightly worse than the S&P Buy-and-Hold strategy. Based on metrics, both its correlation to the buy-and-hold approach (beta) and its edge (alpha) has decreased.

Our Observations​

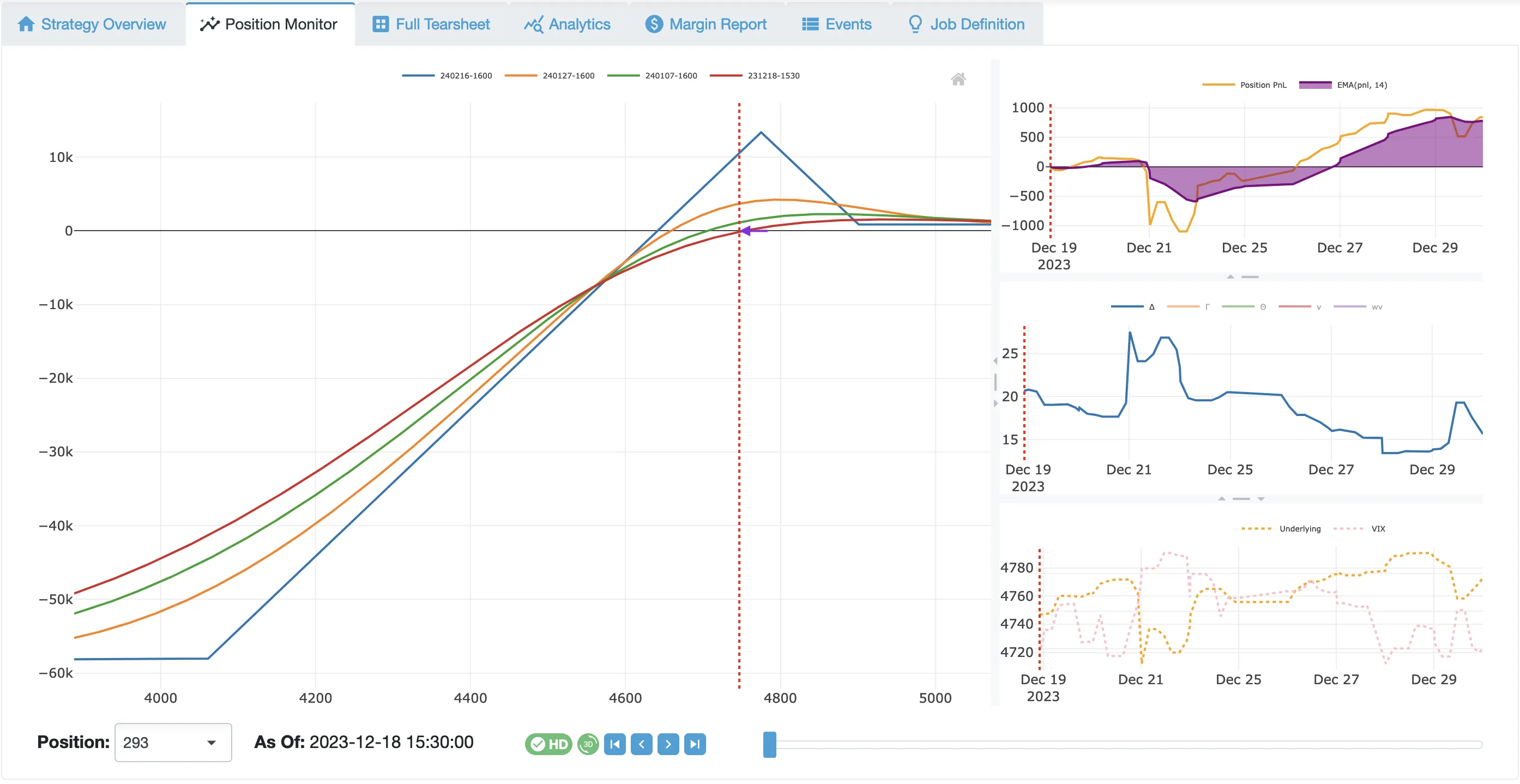
  • Bullish, ATM trade, the position deltas at initiation:
    • Point Map: 25 delta
    • Delta Map: 30 delta
    • Normalized Map: 20 delta
  • Delta Map outperforms Normalized Map:
    The superiority of Normalization over Greeks is not confirmed here.
  • Delta Map shows a substantial correlation (77.69%) with the underlying.
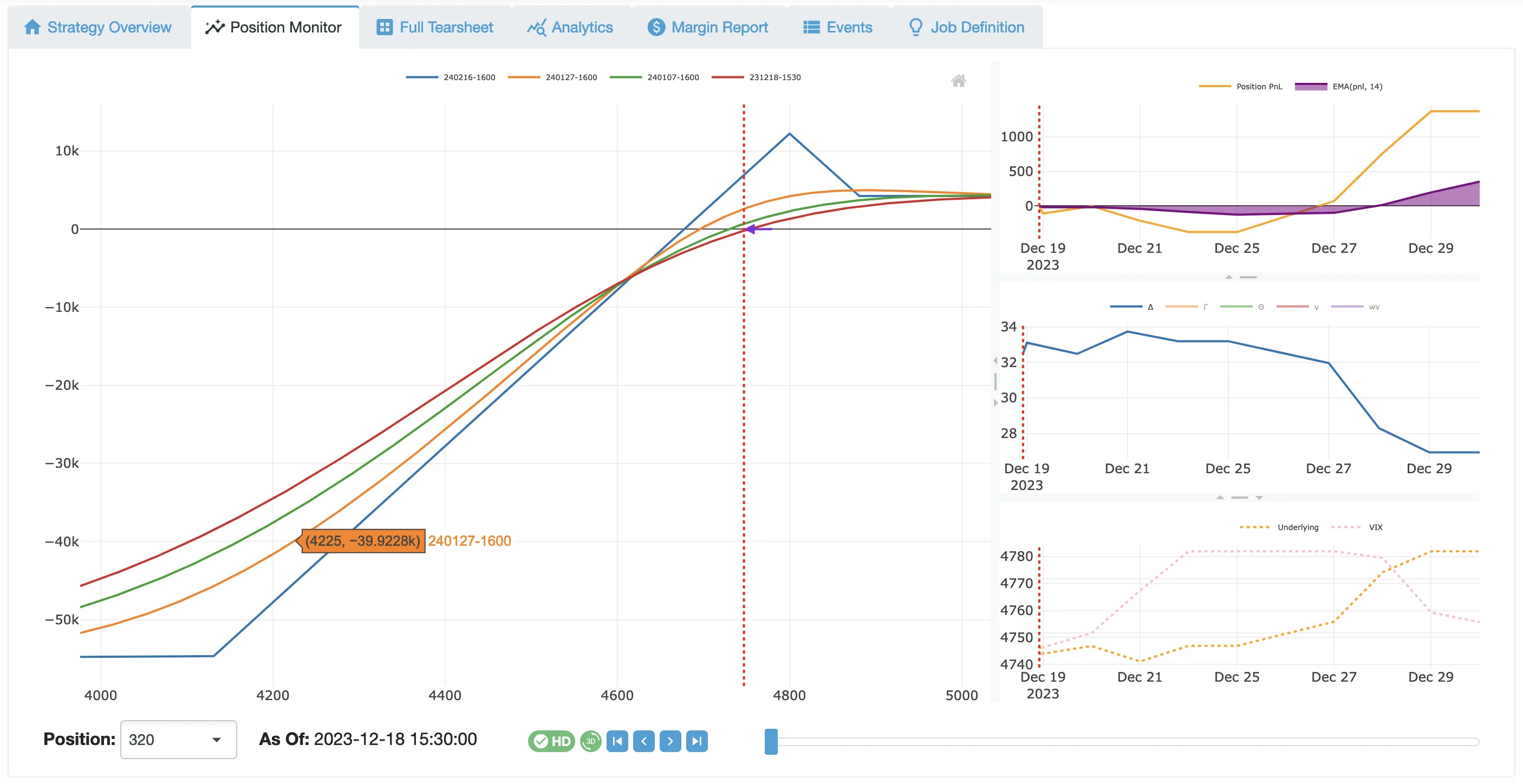
  • ProfitTargets are never reached.
  • Profit plateau is often reached in the first third of the trade.
  • StopLosses are hit in 14% of the trades.
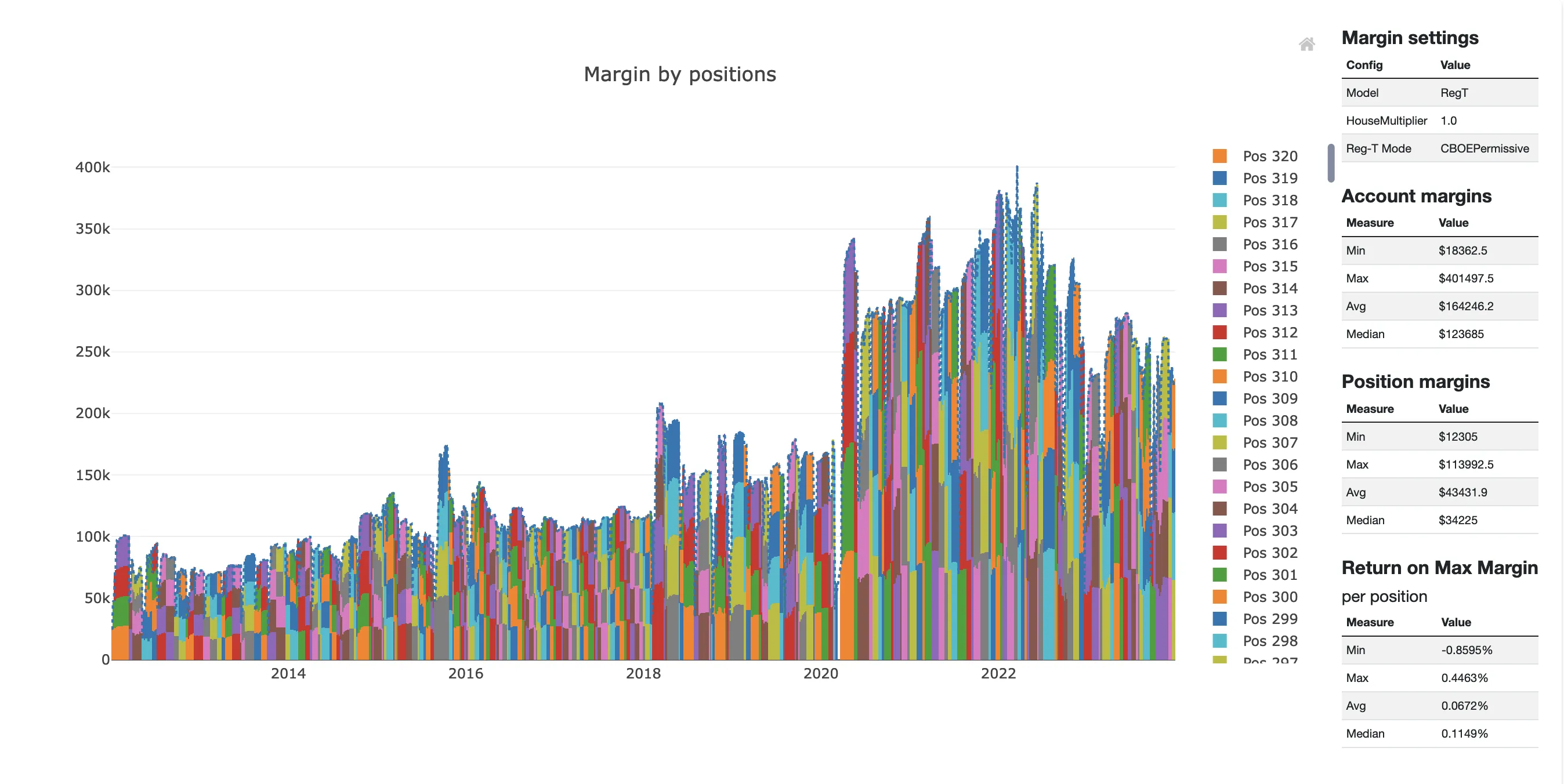
  • The AbortConditions are filtering out the COVID period only.
  • The (RegT) Margin Requirements doubled during the COVID period for the structure.
EvoBWB Delta Map Profit Plateau
EvoBWB Delta Map Entry Aborteds
EvoBWB Delta Map Margin Requirements

Conclusion​

In our attempt to recreate the trades, we concluded that two of the three methods did not provide meaningful improvements over the buy-and-hold strategy. The delta-based approach (Delta Map) offers slightly better performance than the benchmark.

Since the PT targets are not hit and AbortConditions are rarely used, it's evident that the trade is not behaving as expected. This could be due to differences between our implementation and the author's approach, or because the trade didn't stand the test of time. Unfortunately, confirming the former is not possible due to the unavailability of the trade list.

We highly recommend studying the paper, as it provides insights into practical options trading strategies.

Acknowledgments​

We would like to thank David Munoz Constantine, Richard Tymerski and Garrison Greenwood for publishing this trade with a scientific approach.

References​