Delta Hedging Techniques
Intro
Delta hedging aims to eliminate or reduce the risk of price movements in the underlying asset, and it is a common practice among Options Traders.
Nassim Taleb dedicated an entire book, Dynamic Hedging, to the subject of hedging, and we'll cover some aspects of it in relation to MesoSim.
Delta means the sensitivity of a derivative price to the movement in the underlying asset. It is either expressed in percentages or in total amounts. A 50% delta is supposed to mean that the derivative is half as sensitive as the asset and that one needs two dollars in face value of the derivative to replicate the behavior of one dollar of the asset.
Source:
Dynamic Hedging by Nassim Taleb, Chapter 7: Adapting Black-Scholes-Merton: The Delta
Techniques
Delta hedging can be achieved by buying or selling instruments:
- Using options contracts to adjust the structure
- Using a highly correlated asset, such as the underlying, futures contract or related ETFs
- Using more exotic products, such as warrants or swaps
MesoSim supports option 1 out of the box, using Conditional Adjustments. Users can Add, Remove, or Move legs based on various conditions, including position delta. This approach is well documented and demonstrated through built-in templates and public trading strategies. While hedging using options contracts incurs higher costs compared to futures contracts, it offers the advantage of considering other Greeks and metrics during adjustments, making Gamma Hedging a possibility as well.
Options 2 and 3 are also possible in MesoSim by post-processing the event log.
The acc_delta variable can be used to determine how much hedging (in delta terms) is needed.
Since Delta changes as the underlying price moves or time passes, delta hedging requires continuous adjustment. The adjustment frequency depends on the trading strategy. As a rule of thumb: a daily adjustment is a good starting point.
In-depth comparison
In this article we will compare options 1 and 2, using the simplest example, a Strangle:
Non-hedged version
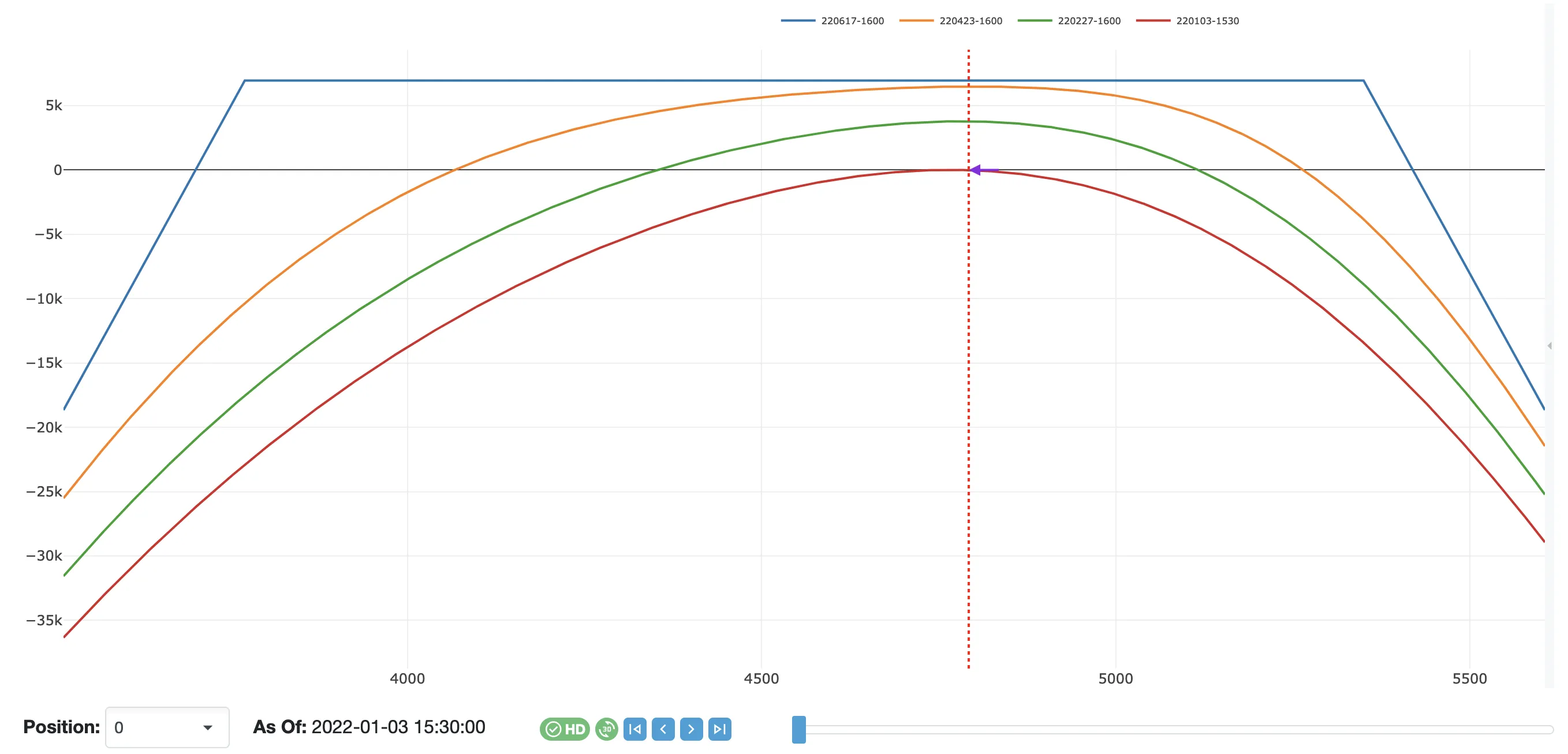
First, we establish our baseline using a 10-delta strangle. No profit target, stop loss, or exit conditions are used in this experiment.
Strategy Performance:
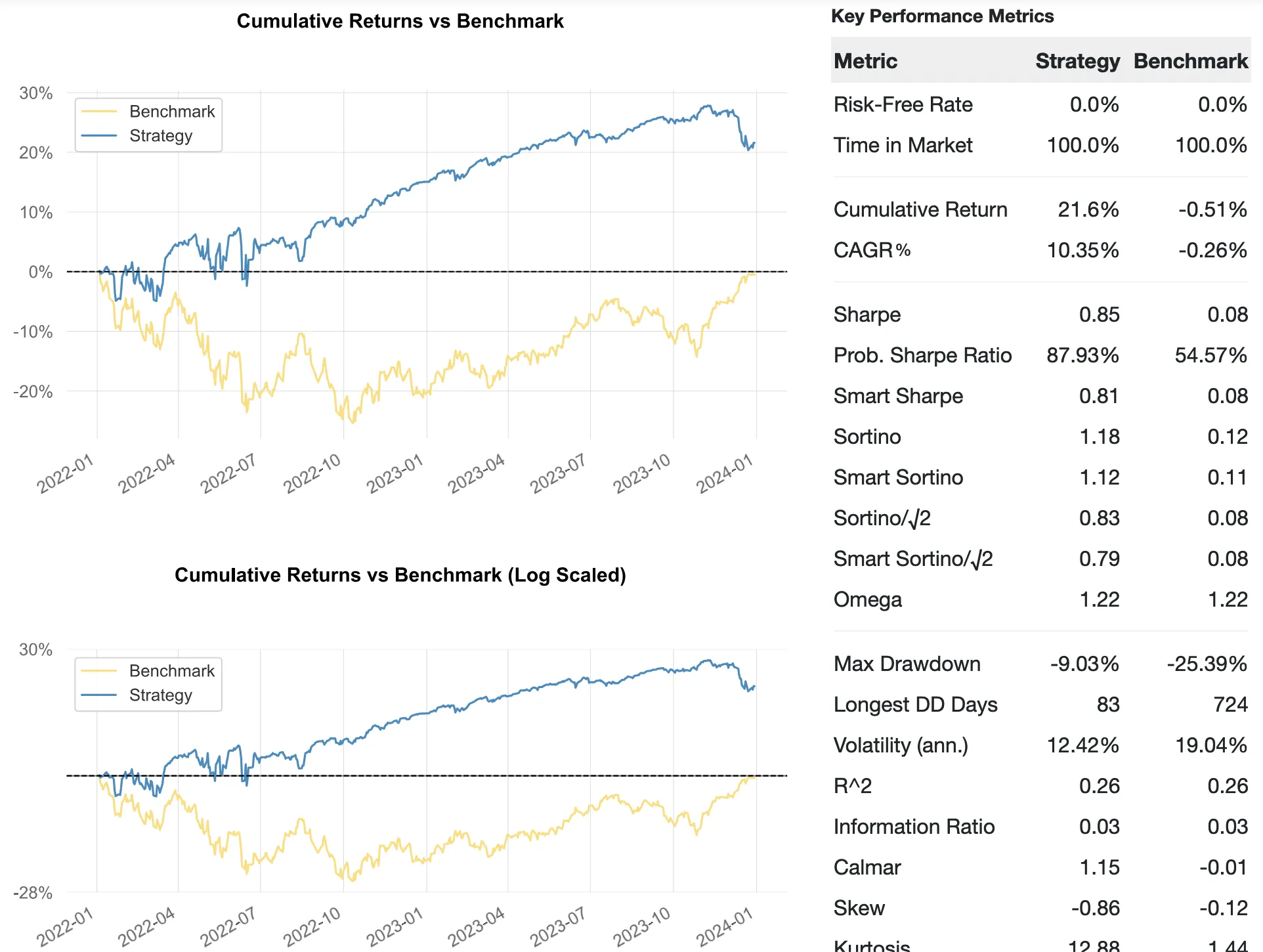
We confirm that the delta of the position indeed varies during the trade lifecycle. Starting with a neutral delta setup (delta=0) as time goes on the delta drifts between +30 and -50, creating signifficant exposure to the underlying price.
The resulting MesoSim run is here
Hedging with Options
Next, we use MesoSim's MoveLegAdjustment to bring the deltas back to neutral when they drift too far. We will refer to this setup as Adjusting.
This technique has been document in detail previously, see the following articles for reference:
The threshold for delta adjustment is set to -5 and 5. Whenever the position delta becomes higher than +5 or lower than -5,
we move the short call and short put legs, respectively, to neutralize the structure's delta.
The resulting job matches our SPX-Strangle-Adjusting built-in template.
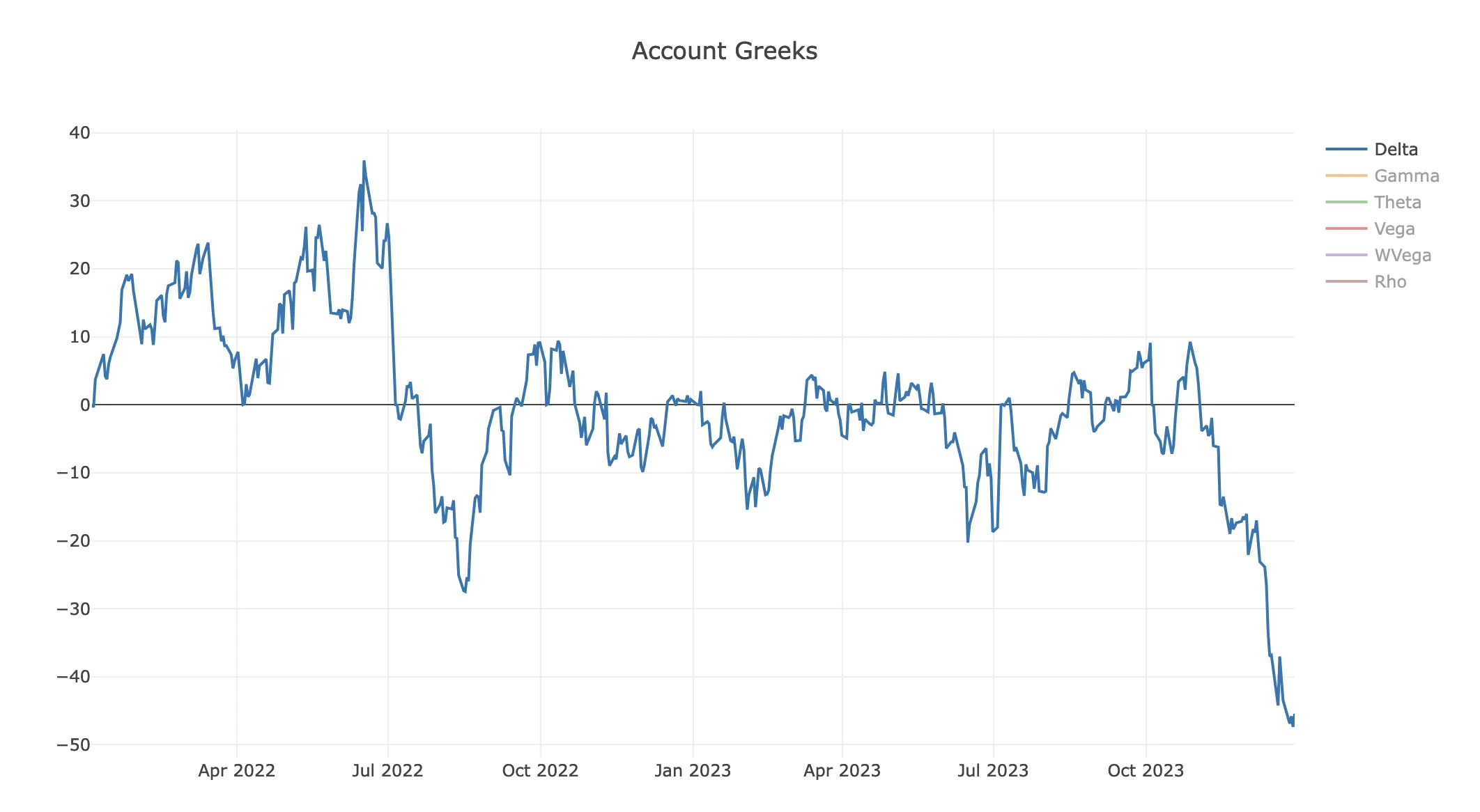
We validate that the account deltas are kept in the range of -5 .. +5 throughout the trade lifecycle:
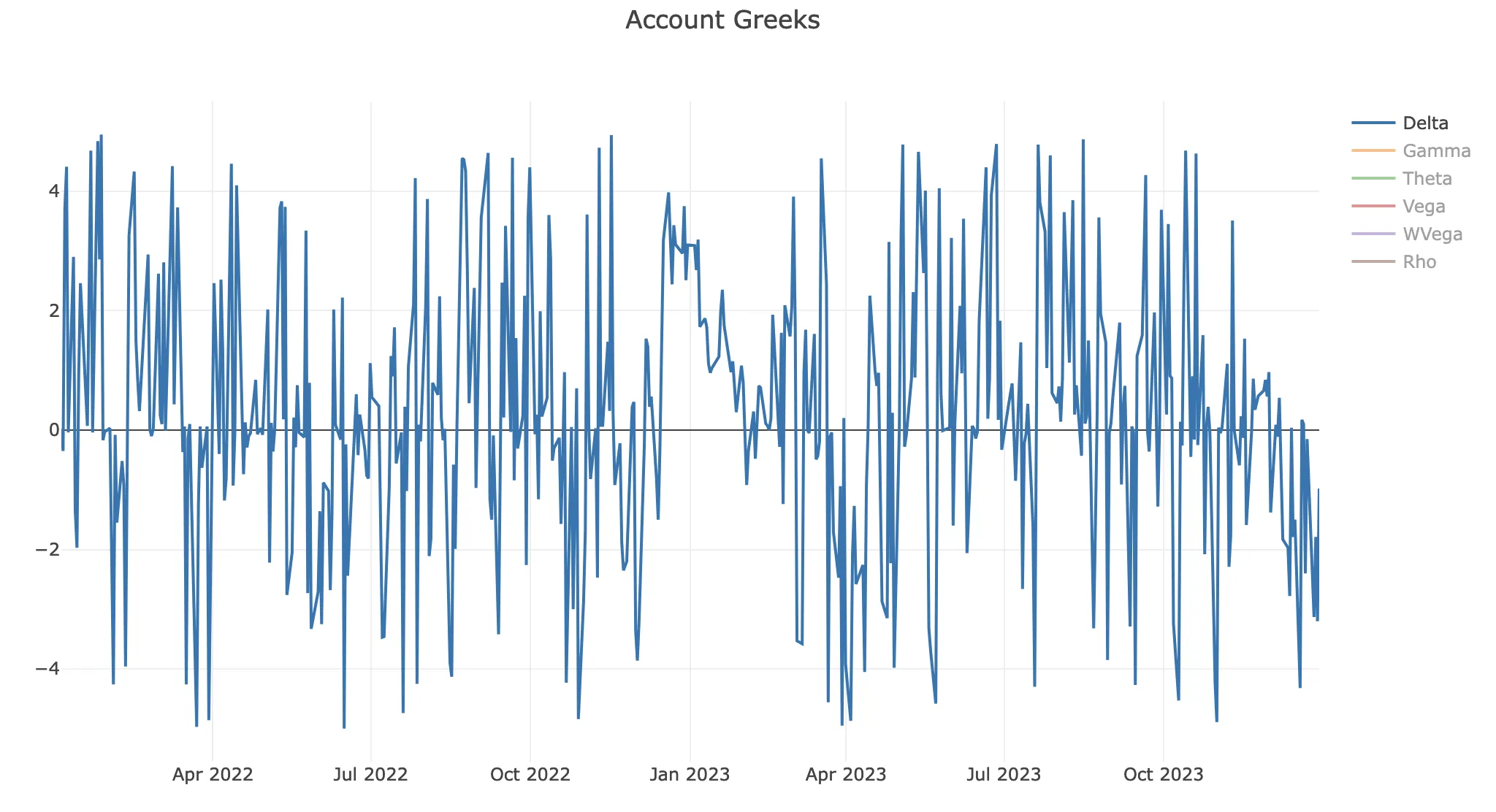
The resulting MesoSim run is here
Hedging with Underlying
To achieve hedging with the underlying asset, we will use Brent Pedersen's delta-hedge.py, shared in his mesosim-stuff repository. We will refer to this run as delta-hedged below.
Brent's approach and implementation are clean and elegant:
He calculates the adjusted PnL series based on the provided delta thresholds on a daily basis.
To make his work more approachable, we converted his code into a Python notebook with the following changes:
- We use Stooq to obtain SPX prices via pandas webreader
- We return a dataframe so that visualization becomes simple
- Q-API is used to render the tearsheet for easy comparison
Please refer to the notebook for further details on the implementation.
We use SPX prices for convenience. SPX is an index that cannot be traded directly.
In practice, hedging can be implemented by buying and selling /ES or /MES futures.
/ES controls 50 contracts, while /MES controls 5, resulting in delta adjustments of 50 and 5, respectively.
The resulting PnL graphs are as follows:
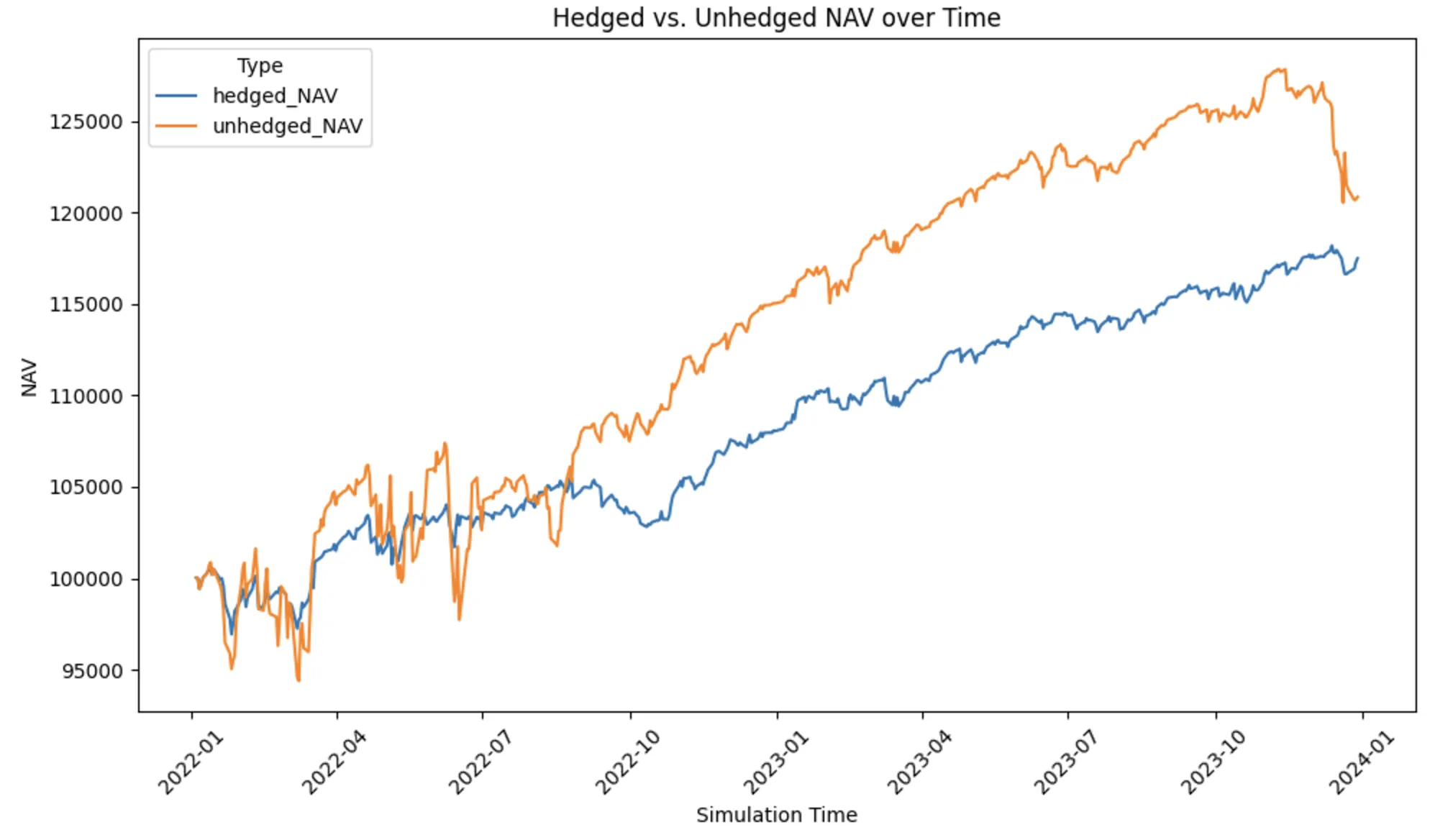
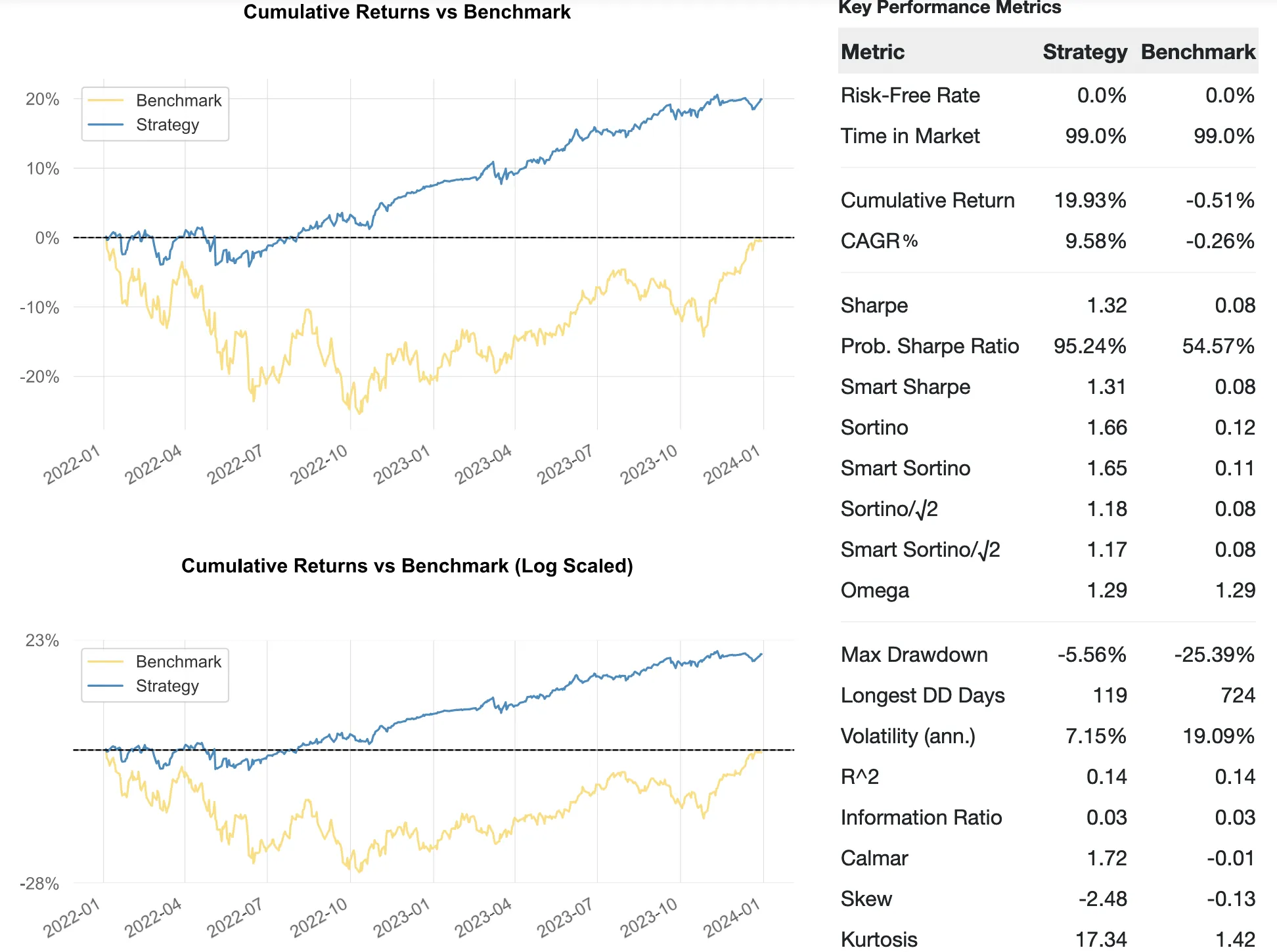
To compare the two approaches, we generate a tearsheet where the strategy represents the delta-hedged (by underlying) approach, and the benchmark is the baseline strangle (without any adjustments):
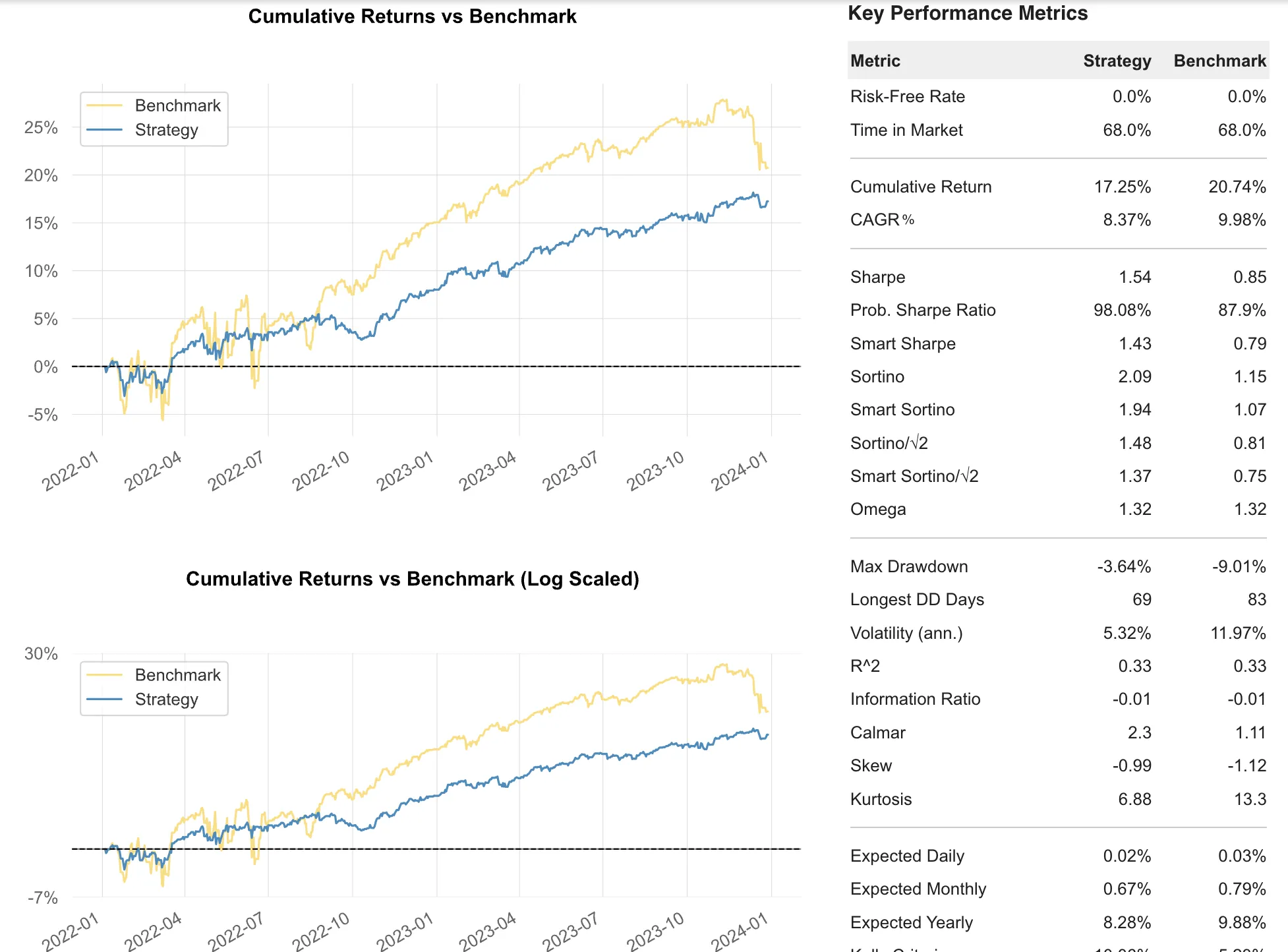
The results are comparable to the Adjusting version.
Conclusion
Both delta hedging approaches yield similar results:
| Experiment | Start | End | CAGR | Max Drawdown | Sharpe |
|---|---|---|---|---|---|
| Baseline | 2022. 01. 01. | 2023. 12. 29. | 10.35% | -9.03% | 0.85 |
| Adjusting | 2022. 01. 01. | 2023. 12. 29. | 9.58% | -5.56% | 1.32 |
| Delta-Hedged | 2022. 01. 01. | 2023. 12. 29. | 8.37% | -3.64% | 1.54 |
The Adjusting approach is supported natively by MesoSim and MesoLive, providing a granular method to keep deltas within range.
The delta-hedged approach can be studied using the provided notebook and easily executed via the brokerage platform.
Acknowledgments
We would like to thank Brent Pedersen for sharing his work related to MesoSim. Be sure to check out his repository for additional MesoSim tools, such as the NAV Combiner, hedging power study tools, and job creators.